An Introduction to Deductive Arguments
11 The Language of Deduction
Section 1: Introduction
In the last chapter, we identified some distinctive features of deductive arguments, and saw that the unique logical strength of deductive arguments is a result of their form. We then looked at a number of common deductive forms, and closed the chapter by identifying two argument forms that are often mistakenly taken to be deductive. In this chapter, we will focus on the language of deduction, specifically on the language of conditionals. As we saw in the last chapter, strict conditionals play an important role in a number of common deductive argument forms. However, we can express conditional relationships in a variety of ways, and this means that we can express common deductive arguments in a variety of ways. As a result, we will be in a better position to spot deductive argument patterns when we run across them. Moreover, some of the lessons we will take from our considerations here will be relevant when we turn to a consideration of the language of inductive arguments.
Section 2: What Strict Conditional Statements Say (and what they don’t)
As we have seen, conditionals are common in everyday reasoning. We can use conditionals in all kinds of ways, e.g. to make promises, threats, or offers, to talk about causal relationships, or to talk about the way things might have been (e.g. “if the Broncos had won Super Bowl XLVIII …”). Given this, let us distinguish between conditionals which are used to describe existing relations—call them conditional statements—and conditionals that are used for other purposes (e.g. conditional promises, conditionals threats, conditional offers, counter-factual conditionals). For the sake of thinking about deductive arguments, we will set aside these other kinds and focus solely on conditional statements. Thus, we will focus on conditionals like the following:
- If sugar is put in the water, then it will dissolve.
- If you are driving without a license, then you are breaking the law.
- If the bird is a mallard, then it is a member of the genus Anas.
And not on conditionals like:
- If you clean the garage, then I’ll lend you the car.
- If you don’t hand over your wallet, then I’ll take it from you.
To this point we have discussed conditional statements as if they were always expressed in the following way: ‘if….then…’. We have called this the Standard Form for conditionals, and have identified the ‘if’ part as the antecedent, and the ‘then’ part as the consequent. However, everyday language is a rich vehicle for expression, and gives us many ways to convey or articulate ideas. Conditional claims are no exception. Because of their importance to deductive arguments, we will identify and discuss some of the most common alternative ways of expressing conditionals.
Towards this end, let us begin by thinking about the relationship(s) that a strict conditional statement expresses. Let’s start with an example we’ve seen before:
Ex. 1:
If a shape is a square, then it is a rectangle.
This strict conditional is claiming that anytime the antecedent is true, and there is a shape that is a square, the consequent is also true: the shape is a rectangle as well. This generalizes to all strict conditionals; they claim that the truth of the antecedent is always accompanied by the truth of the consequent—no exceptions.
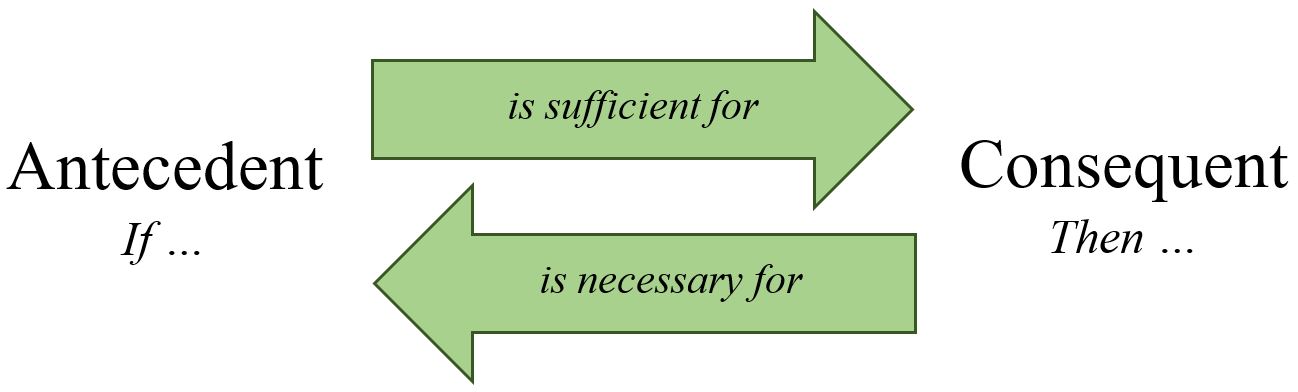
Let us say that a strict conditional claims that the antecedent is sufficient for the consequent because the conditional is saying that knowing the antecedent is true is sufficient for knowing that the consequent is true too, since the one is always accompanied by the other. If the relationship between the antecedent and the consequent in a strict conditional is one of sufficiency, what is the relationship between the consequent and the antecedent? It can be tempting to think that the relationship from the consequent to the antecedent is the same as the antecedent to the consequent, but the example shows us that this is not the case. If a shape is a square, then it is a rectangle, but just because it is a rectangle doesn’t mean it is a square. After all, a square is only one kind of rectangle.

So what is the relationship that the consequent has to the antecedent? Go back to the conditional ‘If a shape is a square, then it is a rectangle.’ This tells us that squares are rectangles, but it also tells us that shapes that are not rectangles also are not squares. After all, since a square is a kind of rectangle, if you knew that shape was not a rectangle you would automatically know that it couldn’t be a square. In other words, it tells us that being a rectangle is a crucial to being a square. We can say, then, that in this case, the truth of the consequent is required, or is necessary for, the truth of the antecedent. This conclusion generalizes to all strict conditionals. In light of this, we will say that in a strict conditional the consequent is necessary for the antecedent.
The fact that the relationship the antecedent has to the consequent is not the same as the relationship the consequent has to the antecedent it is worth emphasizing. According to psychologists and linguists who study reasoning, we have a tendency to misread conditional claims. The problem is that in certain circumstances we read conditionals as if the consequent were sufficient for the antecedent. We tend to read ‘If A, then B’ as saying also that ‘If B, then A’. Of course nobody reads the conditional above about squares and rectangles in this way, because we know that would be false. It is in cases where we aren’t so sure about the antecedent and the consequent that we become prone to making this mistake.[1]
That said, sufficiency and necessity are, in a sense, two sides of the same coin. From the perspective of the antecedent the relation is one of sufficiency for the consequent, while from the perspective of the consequent the relation is one of necessity to the antecedent. More specifically:
A strict conditional of the form if A, then B simultaneously expresses two relations. It says that A is sufficient for B AND that B is necessary for A.
The idea that a conditional expresses two relationships strikes some people as counter-intuitive at first. However, we deal with this situation all the time in everyday life. Consider a different relation: ‘to the left of’. When I say that I am standing to the left of you, I am simultaneously saying that you are standing to my right. So too, to say that A is the grandparent of B is at the same time to say that B is the grandchild of A. The same goes for conditionals—to say that A is sufficient for B is to say simultaneously that B is necessary for A.
Section 3: Necessary and Sufficient Conditions
We began Section 2 by noting that there are many ways to express conditionals other than the standard (if…then…) form. Our discussion of the meaning of conditionals allows us to easily see two alternatives. To say that one thing is sufficient for another, or that one is necessary for the other, is to express a conditional relationship. Consider:
Ex. 2:
A person’s being legally eligible to buy alcohol in this state is sufficient for that person’s being at least 21 years of age.
Because this sentence asserts a sufficiency relation we can express it with a conditional. We can put it into standard form as follows:
If a person is legally eligible to buy alcohol in this state, then they are at least 21 years of age.
There is nothing unique to this example. Using ‘A’ and ‘B’ as variables, we can generalize on this and say that any sentence with the form ‘A is a sufficient condition for B’ can be expressed using the standard-form conditional: ‘If A, then B’ or:
A is sufficient for B = If A, then B
The same goes for necessary conditions. Consider the following example:
Ex. 3:
A person’s being at least 21 years of age is a necessary condition for a person’s being legally eligible to buy alcohol in this state.
Because this sentence asserts a necessity relation we can express it with a conditional. Since ‘a person’s being at least 21 years of age’ is the necessary condition, then it will serve as the consequent in the standard-form conditional, as follows
If a person is legally eligible to buy alcohol in this state, then they are at least 21 years of age.
Again, there is nothing unique to this example. We can generalize on this and say that for a person to say that A is a necessary condition for B is just to express the standard-form conditional: If B, then A or:
A is a necessary condition for B = If B, then A
The conditional above tells us that everybody who is eligible to legally buy alcohol in this state is at least 21—no exceptions. Given this, we can formulate an equivalent variant of this conditional as follows. Consider somebody who is not at least 21 years of age, say they are 19. What do we know about them given the truth of the conditional above? We know that they are not eligible to legally buy alcohol, and we can express this with the following conditional:
If a person is not at least 21 years of age, then they are not legally eligible to buy alcohol in this state.
Being at least 21 years of age is a necessary condition for being legally eligible, so if this necessary condition is not met, it will also be true that a person will not be legally eligible. Again, there is nothing distinctive about this conditional expressed above, and we can say in general that:
If A, then B = If not B, then not A
There is a special name for this equivalent variant of ‘If A, then B’; it is called the contrapositive.
Section 4: Alternative Ways of Expressing Conditionals
There are ways of expressing conditionals beyond the language of necessary and sufficient conditions. Perhaps the most obvious alternative to the standard form occurs when we use the term ‘if’ out of order. For example, a person might say: The bird is a member of the genus Anas, if it is a mallard. The presence of the ‘if’ here is a big clue that we’ve got a conditional, and we can reformulate it into standard form as follows: ‘If the bird is a mallard, then it is a member of the genus Anas’. We can generalize on this:
B, if A = if A, then B
The term ‘only if’ is another way that we sometimes express conditionals. The use of ‘only if’ to express conditionals is especially common in legal language. The word ‘only’ can be tricky, however, and it is important to see that the addition of ‘only’ to an ‘if’ fundamentally changes the meaning of the sentence. Consider the following example:
(i) A person is breaking the law if they are speeding.
(ii) A person is breaking the law only if they are speeding.
These two sentences say very different things. The first sentence says that if a person is speeding, then they are breaking the law. That’s true. The second sentence is telling us that the only way a person might break the law is by speeding. But this is certainly false, since we can break the law by littering, blowing through a stop sign, etc. Adding an ‘only’ to the ‘if’ significantly changes the meaning of the sentence, and so we cannot transform ‘only if’ sentences into standard-form conditionals in the same way we would an ‘if’ sentence. So how do we do it? Let’s look at a new example:
Ex. 4:
A person is considered an “active member” of the club only if they have paid their yearly dues.
This sentence tells us that paying yearly dues is a crucial part of being qualified as an “active member”. Put otherwise if a person hasn’t paid their yearly dues, they are not considered an “active member”. This gives us a standard-form conditional, and we can generalize on this result.
A only if B = If not B, then not A
Now that we also are aware of the contrapositive, we can see that ‘A only if B’ is equivalent to ‘if A, then B’ as follows:
A only if B = if not B, then not A = if A, then B
Perhaps surprisingly ‘all’ and ‘every’ claims like ‘all dogs are mammals’ or ‘every student at this school has been issued an ID card’ express conditional claims as well. In order to see this, think about what they say. To say that every student has been issued an ID card is to say that every single student has an ID card, no exceptions, and so being a student is sufficient for having an ID card. Putting this into the standard form for conditionals requires modifying the sentence a bit (since in standard form conditionals the antecedent and consequent are independent clauses), and this can be a little awkward. We can transform the sentence ‘every student at this school has been issued and ID card’ as follows:
If somebody is a person at this school, then they are a person who has an ID card.
This pattern generalizes and we can say that:
All As are Bs = If something is an A, then something is a B
Claims like ‘all As are Bs’ tell us about membership, namely that things that are As are also members of B. Similarly, claims about exclusion that use ‘no’ or ‘none’ can also express conditionals. For example, to say that ‘no reptiles are warm-blooded’ is to say that all reptiles are not warm-blooded—no exceptions. Put otherwise, being a reptile is sufficient for not being warm-blooded. Like ‘all’ claims, translating a ‘no’ claim into a standard-form conditional requires modifying the sentence structure just a bit. The standard-form conditional in this case is:
If something is a reptile, then it is not warm-blooded.
The general pattern here is:
No As are Bs = If something is an A, then it is not a B
There are other ways of expressing conditionals, but this list captures the most common ways. In the next section, we will see how these alternatives figure into the deductive argument forms we’ve learned.
Section 5: Recognizing Deductive Forms
Being able to recognize conditionals will allow us to recognize instances of the argument forms discussed in Chapter 10. Consider the following argument:
Ex. 5:
Don’t worry, you will graduate. I know that the registrar cleared you, and this is sufficient for graduating.
The claim that being cleared by the registrar is sufficient for graduating expresses a conditional. Transforming this into a standard-form conditional we can see that this argument is an instance of the form Modus Ponens.
- The registrar cleared you.
- If the registrar clears you, then you will graduate.
- So, you will graduate.
Here is another example:
Ex. 6:
Look, I told you—the battery doesn’t have a charge, and the car will start only if the battery has a charge. So, I am sorry to say, the car won’t start.
We know that the claim: ‘the car will start only if the battery has a charge’ expresses the standard-form conditional: ‘if the battery does not have a charge, then the car won’t start’. Given this, we can see that this argument is actually an instance of Modus Ponens, and is consequently a deductive argument.
- If the battery does not have a charge, then the car won’t start.
- The battery does not have a charge.
- So, the car won’t start.
Wait. We have seen that a strict conditional is equivalent to its contrapositive. Thus, in this case although we transformed the claim ‘the car will start only if the battery has a charge’ into the standard-form conditional ‘if the battery does not have a charge, then the car won’t start’ we could have transformed it into a different (but equivalent) standard-form conditional. We might have transformed it to say: ‘If the car starts, then the battery has a charge.’ Had we transformed it this way, we would have standardized the argument as follows:
- If the car starts, then the battery has a charge.
- The battery does not have a charge.
- So, the car won’t start.
But this is a case of Modus Tollens. So which is it? Is this argument an instance of Modus Ponens or Modus Tollens?
The answer, in short, is that it depends on how you transform the conditional claim into standard form. This might seem problematic, but there is no need to worry. How we transform the conditional into standard form will dictate what form the argument takes, but we will never be able to accurately represent a deductive argument as not-deductive if we transform our conditional claims correctly.
Exercises
Exercise Set 11A:
#1:
Identify at least one necessary condition for being a citizen of the United States. You might need to do a little bit of research.
#2:
Identify a necessary condition for getting an A in this class.
#3:
The terms ‘consequent’ and ‘conclusion’ sound very similar. How are they different?
Exercise Set 11B:
Directions: Transform each of the following conditional claims into the correct standard form conditional.
#1:
The chemical will dissolve, if the theory is correct.
#2:
Earning 93% of all available points in this course is sufficient for earning an ‘A’ for the course.
#3:
You may enter only if you are exercising your first amendment rights.
#4:
All submitted photos are the property of Insta.com.
#5:
No current Naval Commanders are convicted felons.
#6:
Having a social security number is a necessary condition for obtaining a driver’s license.
Exercise Set 11C:
Directions: For each of the following arguments standardize it using standard form conditionals and if the argument is one of the kinds we have studied, identify it as such (e.g. Modus Tollens, Affirming the Consequent, etc.)
#1:
Understanding is impossible if words refer only to private sensations in the minds of speakers. We clearly do understand each other. Therefore, words do not refer merely to private sensations.
#2:
Getting a 4 on your AP exam is sufficient for getting college credit. Since I got a 4 on the exam, I will get college credit.
#3:
Future presidents will be allowed to serve a third term only if the Twenty-second Amendment is repealed. The Twenty-second Amendment will not be repealed. Therefore, future presidents will not be allowed to serve a third term.
#4:
Every time Louis is tired, he’s edgy. He’s edgy today, so he must be tired today.
#5:
You can do well in math classes only if you keep up with the assignments. You keep up with the assignments, so you do well in math classes.
#6:
Most senior citizens go to bed before 11 p.m. so my great-grandma probably goes to bed before 11 p.m.
#7:
The alternator is not working properly if the ammeter shows a negative reading. The current reading of the ammeter is negative. So, the alternator is not working properly.
#8:
Manuel will play only if the situation is hopeless. But the situation is hopeless. So Manuel will play.
#9:
Candidate Flores will lose the election if he doesn’t win both Jackson and Northampton County, but he won’t win either of these counties, so Flores will lose the election.
#10:
I passed ‘Go’ and passing ‘Go’ is a sufficient condition for collecting $200, so hand over $200!
#11:
Elephants have been known to bury their dead. Elephants would bury their dead only if they have a concept of death. So, elephants have a concept of death.
#12:
Having a good technical education is a necessary condition for being a good engineer. Given the quality of Charity’s technical education, she will surely make a good engineer.
#13:
We cannot worship a god or gods if we don’t have a capacity to form a concept of the divine. And we cannot have a capacity to form a concept of the divine if we don’t have a capacity to form concepts transcending sense perception. So we cannot worship god or gods if we don’t we have a capacity to form concepts transcending sense perception.
#14:
We know that Philip is a nonresident. Since no citizens are nonresidents, it follows that Philip is not a citizen.
- Wason, P. C., & Johnson-Laird, P. N. (1972). Psychology of Reasoning: Structure and content. Harvard U. Press, 61. ↵
