7 Evaluation and Logical Strength

Section 1: Introduction

Now that we have practiced and refined our argument analysis skills, we can turn to our ultimate goal: argument evaluation.  As we’ve noted, you are already a skilled argument evaluator.  You have a good intuitive sense for the difference between good arguments and bad ones, and our goal is to sharpen these existing skills by taking a closer look at this process.  In the rest of this book we will pursue this aim in three ways.   First, we will develop a vocabulary for talking about argument evaluation.  Second, we will consider a variety of common mistakes in argument evaluation, and thereby put ourselves in a position to avoid making them.  Third, we will identify some useful techniques for evaluating arguments in specific contexts.  As we will see, accurate evaluation often means asking the right questions, and over the next few units we will talk specifically about what kinds of question to ask, and when to ask them.  In this chapter, we take up some important preliminaries to evaluation.  We begin by briefly reviewing the criteria we use to evaluate arguments, and the questions we need to ask in the process. We will then take a closer look at the notion of logical strength, and lay out some important vocabulary for moving forward.

Section 2: Evaluating Arguments

You’ve found an argument, and isolated its premises and conclusion.  Now it is time to evaluate: is it a good argument or a poor one?  Normally, we evaluate arguments in fairly general terms.  We might think “yep, that argument makes sense” or “nope, I don’t buy it.”  However, let’s walk through the process of making this judgment in more detail.  First, recall that we said we’d call good arguments, sound, and poor arguments, unsound.  In a sound argument the premises are true and strongly support the truth of the conclusion.  Consequently, a person can rationally believe the conclusion of a sound argument on the basis of the premises.  In an unsound argument, on the other hand, we cannot rationally believe the conclusion on the basis of the premises.

Given these definitions, there are two ways that an argument can fall short.  First, an argument goes wrong if one (or more) of its premises are false.  After all, a false claim can’t serve as evidence for anything.  Thus, a sound argument cannot have any false premises.  We have a term for this: factual correctness.  As we’ve noted, an argument is factually correct when all its premises are true, and factually incorrect otherwise.  The second way an argument can fall short is when the premises do not offer enough support for the truth of the conclusion.  An irrelevant claim, for example, even if true, is no reason to believe the conclusion.  In a sound argument the premises have to offer strong support for the conclusion.  Again, we have a special term for this characteristic: logical strength.  An argument is logically strong when the premises—if true—provide strong support for the truth of the conclusion, and it is logically weak otherwise.

Because arguments can fall short in terms of factual correctness and logical strength, we need to specifically look for each of these features when we evaluate an argument.  When it comes to factual correctness, we need to look at each premise and ask: is this likely to be true?  When it comes to logical strength, we need to ask: is the conclusion probable assuming the truth of the premises?  If your answer to all these questions is ‘yes,’ then you should deem the argument sound.  If your answer to one is ‘no’ then unsound, and if you are not in a good position to say one way or the other, then you can only step back, admit you don’t know, and wait for more information.

The Two Key Evaluative Questions:

Are the premises likely to be true?

Is the conclusion probable given the truth of the premises?

With this terminology in hand, let’s walk through a few cases to illustrate the evaluative process in action.  Ava has just met Greg.  She mentions to this to a friend who says:

Ex. 1:

“I don’t know him, but I think he is on the tennis team; I stopped by his dorm room once to borrow something from his roommate, and noticed that Greg has a tennis racket.”

Ava’s friend has just given the following argument:

1) Greg has a tennis racket.

2) So, Greg is on the tennis team.

Presented with this argument, Ava turns to evaluation.  She thinks to herself: I don’t buy it.  Yeah, I have seen that he has a tennis racket too, so the premise is true; but I don’t see how that makes it probable that he is on the tennis team. Tennis is a popular pastime, and many people play tennis without being on a team.  So, although I agree that the argument is factually correct, I ultimately think the argument is unsound because it is logically weak.

This example provides an opportunity to emphasize that in saying an argument is unsound, we are not thereby saying the conclusion is false.  The fact that Greg has a tennis racket doesn’t give a good reason for thinking that he is on the tennis team.  That said, neither does it rule it out.  In judging that the argument in Example 1 is logically weak Ava is saying only that the evidence provided isn’t good enough for believing Greg is on the tennis team, and barring additional information, we can’t say one way or the other.  Let’s consider a different example.  Ava and a friend are looking through the course offerings for next semester, and her friend says:

Ex. 2:

“Hey, we could take neuroscience of gender, that sounds cool.  Wait. I take it back; we can’t sign up for the course since it has BIO 2 as a prerequisite, and we haven’t taken that yet.”

Ava’s friend has just given the following argument:

1) The course has BIO 2 as a prerequisite.

2) We haven’t taken BIO 2.

3) So, we can’t sign up for the course.

Turning to evaluation, Ava thinks to herself: that’s not right.  I agree that if BIO 2 were a prerequisite, we wouldn’t be able to sign up for the course, since neither of us have taken BIO 2.  The problem is that BIO 2 is not actually a prerequisite (Ava got an email from her advisor earlier in the day noting a number of mistakes in the course listings, including this one).  So, while the argument is logically strong, it is unsound because it is factually incorrect.

In both of these cases, Ava has been presented with an opportunity to update her system of belief with new information.  Moreover, in each case Ava used the Key Questions to methodically think through each argument.  In both cases she judged the evidence to be lacking: in the first case because it was logically weak and did not support the conclusion strongly enough, and in the second case because it was not factual correct.  As a result of these judgments, she rejected the proposed additions to her system of belief.

Let us consider one more case.  In the following example Ava’s friend is talking about a proposed state law that would require all motorcyclists to wear helmets.  Her friend disagrees with the proposal, and says:

Ex. 3:

“This is a clear case of government overreach since it infringes on an individual’s right to accept the risks of riding without their helmet.”

Ava’s friend has just given the following argument:

1) The proposed law infringes on an individual’s right to accept the risks of riding without their helmet.

2) So, the proposed law is a case of government overreach.

Ava thinks to herself: that doesn’t seem right.  On the one hand, the premise is true—the law does infringe on motorcyclists’ right to choose whether or not to wear a helmet.  But all by itself this doesn’t mean the law is a case of government overreach.  It seems like there are other relevant factors here.  A helmet is not only a fashion choice— it concerns matters of life and death.  Wearing a helmet can save a person’s life in a crash and prevent irreparable brain damage.  I mean most states have seatbelt laws, and these laws infringe on an individual’s right without counting as government overreach, right?  As a result, I think this argument is logically weak—the mere fact that a law infringes an individual’s right does not mean it is a case of government overreach.  

This example is different from the previous ones, and raises some interesting questions.  Although we might not know whether Greg is on the tennis team or not, or whether BIO 2 is really a prerequisite, there are clear and commonly accepted ways to settle these issues by determining the facts of the matter (e.g. checking with the tennis coach or team members, asking the instructor or registrar’s office).  But this case is not so clear.  How do we determine whether this is “government overreach” for example?  There is no easy and commonly accepted procedure to answer this question.  Indeed, although Ava thinks this argument is unsound, it is not difficult to imagine others arriving at the opposite conclusion.  Perhaps, for example, they would say that seatbelt laws are cases of government overreach as well.  How can Ava be sure that her evaluation is right?

In thinking about cases like this it is important to begin with an observation: the world is complex and in a state of constant change.  This can make it difficult to understand the world and its contents, since doing so often requires integrating disparate pieces of information—information that itself can be complex and changing.  Put differently, some subjects are difficult and complicated, and accordingly there may be no simple, easy, or obvious way to evaluate arguments about them.  Indeed, we are called upon to evaluate ideas, arguments, and proposals in these circumstances commonly.

Moreover, when issues are complicated in this way, we should expect disagreement or controversy.  Think about it: when we evaluate arguments we do so from our perspective and in light of our system of beliefs.  The more complex an issue is, the more likely that two or more people will not share all the same beliefs about it.  In these cases, it is common for one person to know something the other person does not.  This also shows that disagreement, all by itself, does not mean you are wrong, or that there is no fact of matter.  After all, this disagreement may grow out of misunderstanding, ignorance, or mistaken reasoning (we will talk more about disagreement in Chapter 18).

To return to Ex. 3, Ava is evaluating this argument in light of what she takes herself to know about the world, and from her perspective the argument seems logically weak.  Nevertheless, she might be wrong. Maybe her friend knows something she doesn’t.  Perhaps there are good reasons to think that the rights of motorcyclists outweigh concerns about their safety.  But in the absence of any positive information to this effect, it makes sense for Ava to evaluate the argument as unsound.  That said, her evaluation of the argument is not fixed.  Because Ava recognizes that the world is complicated and she may have missed something, she keeps an open mind, and is willing to adjust her views in light of new information or arguments.  Indeed, this would be a good opportunity for cooperative dialogue with her friend as a way to learn more about why her friend disagrees as well as to share her perspective.

As a final point, let us consider a comparison that may be useful for conceptualizing argument evaluation: a baseball umpire.  An umpire has standards for calling strikes, fair and foul balls, and whether a runner is safe or out (among others things).  These standards tell an umpire what to be looking out for in certain situations.  Moreover, some events may be more difficult to call than others, and it takes practice to learn how to consistently apply these standards.  Nevertheless, even the calls of experienced umpires are subject to error and controversy from time to time.  In some cases, the situation is ambiguous or difficult to decide. In other cases, an umpire might not be in a good position to see something relevant, and sometimes umpires simply make a mistake.  Evaluating arguments is similar.  In evaluating an argument our job is to put the standards of factual correctness and logical strength to work.  These standards tell us what we should be looking for, and the questions to ask.  Some arguments are more difficult than others to evaluate, and it takes practice to learn how to apply them well.  Further, like an umpire, sometimes we are faced with ambiguity or disagreement, are missing some crucial piece of information, or simply make a mistake.  There is an important difference, however.  Unlike the umpire we do not have to make a call.  That is, we don’t have to say ‘factually correct’ or ‘factually incorrect’, or ‘sound’ or ‘unsound’.  In most cases, we can simply admit that we don’t know, and need more information before we can say one way or the other.  We will have more to say about the process of evaluation as we proceed through the coming chapters.  For now, let us take a closer look at one of the key concepts in argument evaluation, logical strength.

Section 3: Degrees of Logical Strength

As we’ve seen, an argument is logically strong when the premises—if true—give strong support for the truth of the conclusion, and logically weak otherwise.  Logical strength is not all or nothing; it is a variable characteristic of arguments that comes in degrees.  That is, one set of premises might offer more or less support for a conclusion than another.  As we will see, this is important because it allows us to distinguish different kinds of arguments, and argumentative standards.

Let’s take a closer look: imagine degrees of logical strength on a scale that runs from 0 on the left to 100 on the right.  Let 0 represent the absence of logical strength, and 100 represent maximal logical strength.  In an argument with no logical strength, the truth of the premises is wholly unrelated to the truth of the conclusion.  We don’t see arguments like this too often, but here is an example:

Ex. 4—Logical Strength 0:

Since Harrisburg is the capital of Pennsylvania, the Denver Nuggets will probably make the NBA playoffs this year.

This is a total non sequitur (Latin for “does not follow”): which city is the capital of Pennsylvania tells us nothing about the NBA playoff picture. Moving up the scale from 0, we have arguments whose logical strength lies somewhere between 1 and 50.  In these arguments the truth of the premises would give some reason to believe the conclusion, but would not make it probable.  For example, suppose that a painting has been stolen, and Lucy’s fingerprints have been found at the scene of the crime.  The fact that Lucy’s fingerprints were found at the scene of the crime is relevant and gives some reason to think that she committed the crime, but does not make her guilt probable all by itself, since there may be other reasons her finger prints were found there.   That is, it would be logically weak to argue:

Ex. 5—Logical Strength 1-50:

Since Lucy’s fingerprints were found at the scene of the crime, she is probably guilty.

Because the fingerprint is only suggestive, we’d need more evidence to conclude that she probably committed the crime.  Continuing up the scale, let us imagine that 50 is the tipping point or threshold for strong arguments.  In arguments with a logical strength of 51-99 the truth of the premises makes it probable that the conclusion is true.  These are logically strong arguments, and most of the logically strong arguments we run across fall within this range.  To give an everyday example, you’ve got a really sore throat and go to your trusted family doctor.  The doctor does a quick test and tells you that you’ve got strep throat, and prescribes some antibiotics.  In this case, it would be logically strong to reason:

Ex. 6—Logical Strength 51-99:

Since the doctor says I have strep throat, I probably have strep throat.

In this example, your doctor is a trusted expert whose job involves accurately diagnosing and communicating with patients, and this gives you good reason to conclude you’ve got strep. This brings us, last, to maximal support at 100. In these arguments, the truth of the premises guarantees the truth of the conclusion. Put differently, in an argument with maximal logical strength the conclusion cannot be false if the premises are true.  To illustrate:

Ex. 7—Logical Strength 100:

We can be sure that all whales have livers, since all whales are mammals and all mammals have livers.

In this case, if it is true that all mammals have livers and that all whales are mammals, it cannot be false that whales have livers.  Though arguments like this are not particularly common in everyday life, they are very important.  As it turns out, arguments with maximal logical strength have a number of interesting and useful characteristics, not the least of which is that their conclusions can be known with certainty (if their premises are true).  In fact, there is a whole discipline called ‘Formal Logic’ dedicated to the study of this kind of argument.  Because of their distinctiveness, arguments with maximal logical strength are used as a basis for classifying arguments more broadly.  Thus, arguments with maximal logical strength are called deductive arguments, and arguments with less than maximal logical strength are called inductive arguments.  Let us say that:

An argument is deductive when (and only when) it is maximally logically strong insofar as the truth of the premises guarantees the truth of the conclusion.

An argument is inductive when (and only when) it is less than maximally logical strong insofar as the truth of the premises does not guarantee the truth of the conclusion.

It is important to draw one more set of distinctions when it comes to inductive arguments.  After all, just because the truth of an argument’s premises does not guarantee the truth of its conclusion, doesn’t mean it is a weak argument.  We regularly and effectively reason using arguments in which the truth of the premises makes the truth of the conclusion probable without guaranteeing its truth.  Thus, we can distinguish between those inductive arguments that are logically strong, and those that are logically weak.  We will say that the former are inductively strong, and the latter are inductively weak.

Given these distinctions, we can classify all arguments in terms of their logical strength.  In the following diagram ‘LS’ stands for logical strength.

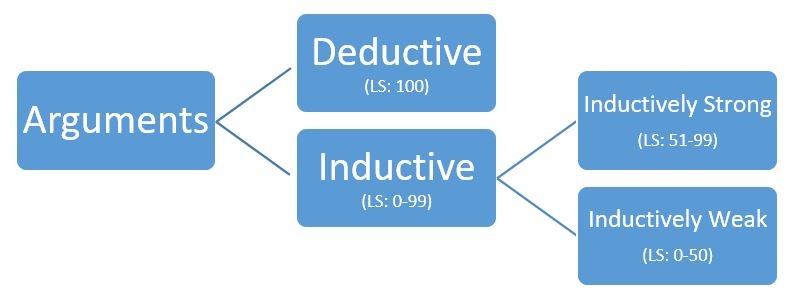
Why does this matter?  Different levels of logical strength are appropriate for different circumstances, and we seek to create and evaluate arguments of differing strength accordingly.  Although we can find deductive arguments in many contexts, they are most common in mathematics.  For example, think back to high school geometry class.  Suppose that you’ve been assigned the task of proving that every angle has a unique bisector.  Success, in this case, is a matter of coming up with a deductive argument for this conclusion, and that is what you’ll try to offer.  However, most contexts do not call for such a high degree of logical strength, and most of the arguments we use and run across are intended to be merely inductively strong.  Nevertheless, this distinction means that we need to keep in mind that some arguments are crafted to be deductive, and should therefore be evaluated by the standard.  Similarly, some arguments are crafted to be only inductively strong, and should therefore be evaluated by that standard.  To illustrate the worry, go back to Ex. 6.  Imagine a critic objecting: “this is a poor argument, after all, it is possible that you don’t have Strep throat even though the doctor said you do.”  To object in this way, is to apply a deductive standard to a case in which an inductive standard is appropriate.

How do we figure out what standard is appropriate?  Context will help, of course, but the most straightforward way is in terms of indicator words.  When a speaker or author intends an inductively strong argument, they will commonly qualify their conclusions by saying that they are ‘probable’ or ‘likely’ or that the conclusion ‘seems to follow’.  Similarly, when a speaker or author intends a deductive argument, they will commonly indicate this by saying that the conclusion must be true, that it necessarily follows, that it is proven, etc.  Of course, there are many different ways to express that a conclusion is likely or necessary, and we cannot look at every possible synonym.  It will be enough for our purposes to note that i) authors and speakers often make this qualification and ii) that this qualification gives us a guide for thinking about the standards by which to evaluate the argument.  If an argument is offered as a proof, then it must have perfect logical strength—anything less qualifies it as a deductive failure.  If an argument is offered with a recognition that the argument is not conclusive, then the standard of inductive strength is appropriate.  There is a lot more to say about both deductive and inductive arguments, and we will discuss these topics in detail later.

Exercises

Exercise Set 7A:

#1:

Create a standardized argument that is logically strong, but factually incorrect.

#2:

Create a standardized argument that is logically weak, but factually correct.

#3:

Create a standardized argument that is logically strong, but has a false conclusion.

Exercise Set 7B:

Directions: Decide whether the following arguments are intended to be deductive or inductive, and then try evaluating the argument by that standard of logical strength.

#1:

I doubt Callista will be at Spin class, since she broke her ankle last week.

#2:

We know that either the Butler or the Chauffer committed the murder, but it can’t have been the Butler since he was 20 miles away at the time of the murder.  So, it must have been the Chauffer.

#3:

Both Alex and Hakim live in Philadelphia; I bet they go to the same dentist.

#4:

Vaughn is an employee; so he must have access to office, since everyone who has access to the office is an employee.

Exercise Set 7C:

Directions: Evaluate the following arguments for soundness.  In making your judgment, please explicitly comment on the argument’s factual correctness and logical strength.

#1:

Since Ottawa is the capital of Canada, it is probably Canada’s most populous city.

#2:

The multiples of 3 are all odd, since 3 is an odd number and every multiple of an odd number is itself odd.

#3:

An inductively weak argument is one whose premises, if true, do not make the conclusion probable.  If the premises, even if true, do not make the conclusion probable, then the conclusion is false.  So, inductively weak arguments always have a false conclusion.

#4:

Many books have already been digitized, and there is a digital version of almost every new book that is published.  Because of this, brick and mortar libraries will likely become obsolete in coming years.

#5:

Smoking and vaping should be legally banned in all their forms, since both smoking and vaping are bad for your health.

#6:

Christopher Columbus initiated the colonization and subjugation of indigenous peoples of the Americas, and these are not the actions of a man who should be honored or commemorated in our public spaces. Consequently, we have a duty to remove monuments of Columbus from public spaces.

Exercise Set 7D:

#1:

As you were evaluating the arguments in exercise set 7C, what questions or problems did you have?  If you didn’t have any questions or problems, what are some questions other people might have in completing these exercises?

#2:

In order to find a defendant guilty in a criminal trial, jurors need to believe the evidence shows guilt “beyond a reasonable doubt.”  Understood in terms of logical strength, what degree of logical strength is “beyond a reasonable doubt?”  Explain.